ディープラーニングの歴史を振り返ってみようと思い、前回のAlexNetに続いてVGG16について自分なりに整理します。
現在私がPyTorchの勉強をしているので、ここから先のコードはPyTorchベースとなる点、ご了承下さい。
元となる論文はこちらですので、詳細が気になる方はぜひ一読してみてください。
VGG16の構造を理解するために、PyTorchでの実装を見てみます。
class VGG(nn.Module):
def __init__(
self,
features: nn.Module,
num_classes: int = 1000,
init_weights: bool = True
) -> None:
super(VGG, self).__init__()
self.features = features
self.avgpool = nn.AdaptiveAvgPool2d((7, 7))
self.classifier = nn.Sequential(
nn.Linear(512 * 7 * 7, 4096),
nn.ReLU(True),
nn.Dropout(),
nn.Linear(4096, 4096),
nn.ReLU(True),
nn.Dropout(),
nn.Linear(4096, num_classes),
)
if init_weights:
self._initialize_weights()
def forward(self, x: torch.Tensor) -> torch.Tensor:
x = self.features(x)
x = self.avgpool(x)
x = torch.flatten(x, 1)
x = self.classifier(x)
return x
def _initialize_weights(self) -> None:
for m in self.modules():
if isinstance(m, nn.Conv2d):
nn.init.kaiming_normal_(m.weight, mode='fan_out', nonlinearity='relu')
if m.bias is not None:
nn.init.constant_(m.bias, 0)
elif isinstance(m, nn.BatchNorm2d):
nn.init.constant_(m.weight, 1)
nn.init.constant_(m.bias, 0)
elif isinstance(m, nn.Linear):
nn.init.normal_(m.weight, 0, 0.01)
nn.init.constant_(m.bias, 0)
def make_layers(cfg: List[Union[str, int]], batch_norm: bool = False) -> nn.Sequential:
layers: List[nn.Module] = []
in_channels = 3
for v in cfg:
if v == 'M':
layers += [nn.MaxPool2d(kernel_size=2, stride=2)]
else:
v = cast(int, v)
conv2d = nn.Conv2d(in_channels, v, kernel_size=3, padding=1)
if batch_norm:
layers += [conv2d, nn.BatchNorm2d(v), nn.ReLU(inplace=True)]
else:
layers += [conv2d, nn.ReLU(inplace=True)]
in_channels = v
return nn.Sequential(*layers)
cfgs: Dict[str, List[Union[str, int]]] = {
'A': [64, 'M', 128, 'M', 256, 256, 'M', 512, 512, 'M', 512, 512, 'M'],
'B': [64, 64, 'M', 128, 128, 'M', 256, 256, 'M', 512, 512, 'M', 512, 512, 'M'],
'D': [64, 64, 'M', 128, 128, 'M', 256, 256, 256, 'M', 512, 512, 512, 'M', 512, 512, 512, 'M'],
'E': [64, 64, 'M', 128, 128, 'M', 256, 256, 256, 256, 'M', 512, 512, 512, 512, 'M', 512, 512, 512, 512, 'M'],
}
def _vgg(arch: str, cfg: str, batch_norm: bool, pretrained: bool, progress: bool, **kwargs: Any) -> VGG:
if pretrained:
kwargs['init_weights'] = False
model = VGG(make_layers(cfgs[cfg], batch_norm=batch_norm), **kwargs)
if pretrained:
state_dict = load_state_dict_from_url(model_urls[arch],
progress=progress)
model.load_state_dict(state_dict)
return model
def vgg16(pretrained: bool = False, progress: bool = True, **kwargs: Any) -> VGG:
return _vgg('vgg16', 'D', False, pretrained, progress, **kwargs)図で表すとこのようになります。
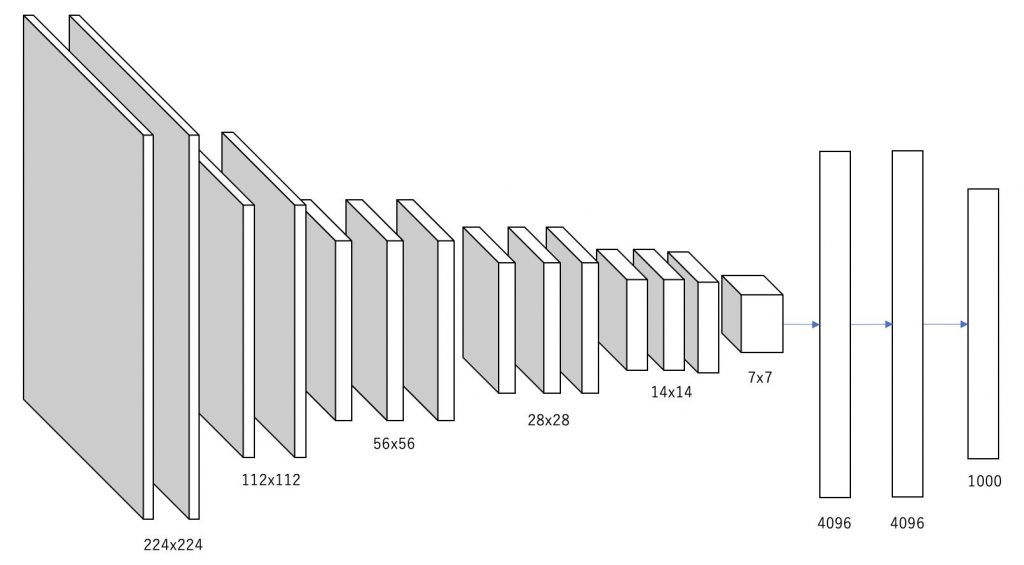
ソースコードと図からわかる通り、13枚の畳み込み層と3枚の全結合層から構成されています。今回引用したソースはVGG16以外にもVGG11やVGG13、VGG19にも対応できるようになっているので、汎用的な作りになっています。(参考になる!)
ちなみに畳み込み層と全結合層の間にある「AdaptiveAvgPool2d」はAlexNetと同じように入力のサイズが何であれ出力のサイズを$(7 \times 7)$に合わせる役割となっています。入力画像のサイズが$(224 \times 224)$であれば畳み込み層を通過した時点で$(7 \times 7)$のはずですが、入力画像のサイズが異なる場合でも対応できるようになっています。
論文ではVGG16だけでなく、層を増やした場合(VGG19)や減らした場合(VGG11、VGG13)の挙動について触れています。以下図はそれぞれどのような構造であるかを表したものです。
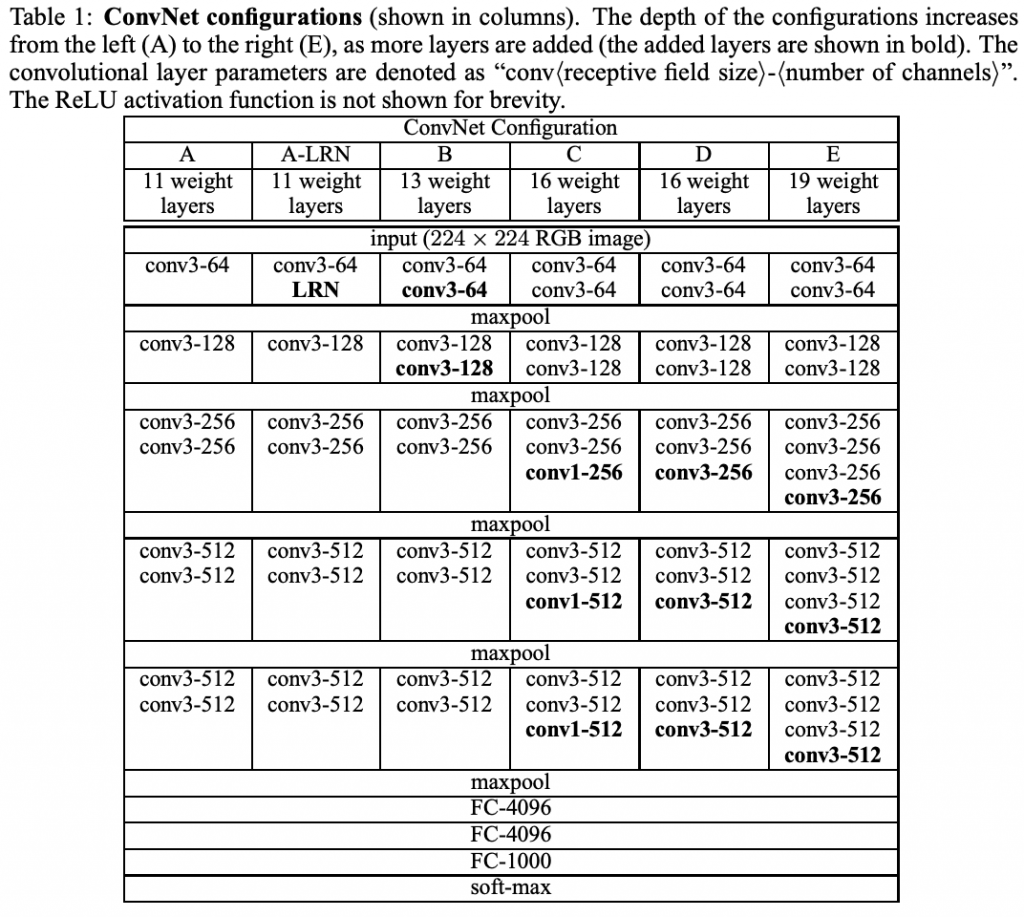
そして、以下表は、各パターンに対してtrainデータとval&testデータの画像サイズや評価手法を変化させた場合のvalデータのTop1とTop5のエラー率です。
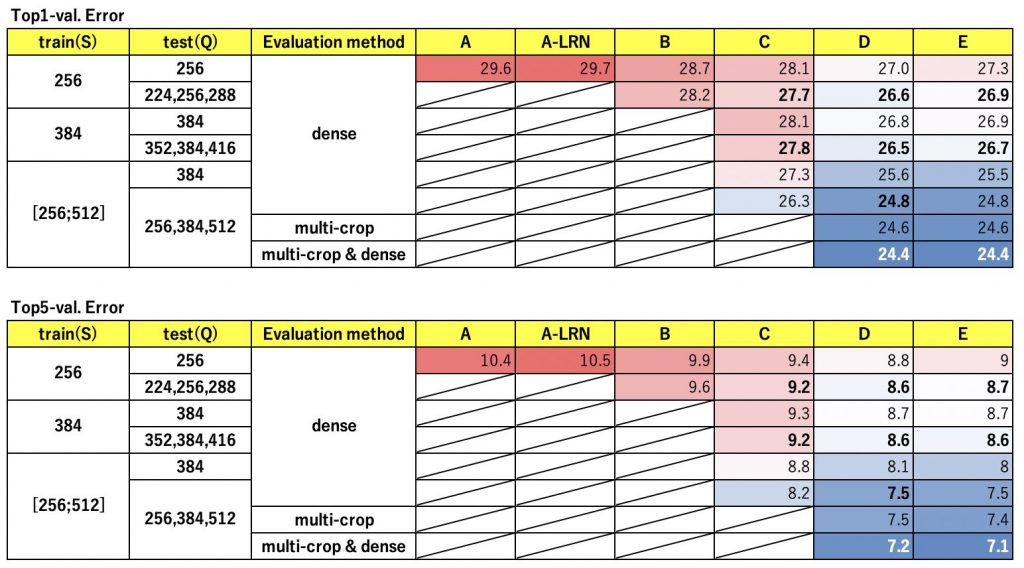
この結果について簡単ですが補足します。
trainデータの画像サイズが[256;512]になっている部分は、画像サイズを256から512の間でランダムにリサイズすることを表しています。これにより画像の中で分類したいオブジェクトのサイズ違いを吸収できるようです。
testデータの画像サイズが複数になっている部分は、複数の画像サイズで評価した結果の平均を取ります。
評価手法についてはそれぞれ以下です。
- dense:1枚の画像に対して1回評価する。
- multi-crop:1枚の画像に対してクロップすることで複数回評価する。
AlexNetで登場したLRNについては、この論文では精度の観点で有効性が無かったと判断されています。
黒太字は論文著者がILSVRCで提出した組み合わせで、Top1-val. Error 24.7、Top5-val. Error 7.5になったようです。
白太字は論文著者がILSVRC終了後に色々試して叩き出したベストスコアの組み合わせで、Top1-val. Error 23.7、Top5-val. Error 6.8になったようです。
ここまでの結果からVGGでベストスコアを出す条件はこちらになりそうです。
- 層が厚ければ厚いほど精度が上がるが、計算コストを鑑みると必ずしもVGG19がベストというわけではなさそう。
- LRNは使わない。
- trainデータはランダムにリサイズする。
- testデータは複数サイズで評価した結果の平均を取る。
- 評価する際はdenseとmulti-cropを組み合わせる。
まとめ
現在ではVGG16はパラメータ数が多いが精度は劣っているので使われることはあまり無さそうですが、改めて振り返ってみることで得るものがある気がしました。次はさらにVGG16よりも進化したモデルについて調べてみようと思います。